銀行など、金融機関に預けたお金には利子がつきますが、利子の種類は一つではないことを知っていますか？大きく分けると「単利」と「複利」という種類に分けることができます。

相対性理論で有名な物理学者、アルバート・アインシュタインがお金にまつわる有名な言葉を残しています。

「複利は人類による最大の発明だ。知っている人は複利で稼ぎ、知らない人は利息を払う」

この言葉は、貯金や投資をする時の利息や利子などの増え方を表したものだと考えられます。今回はこの「複利」の特徴や仕組み、効果について、単利と比較しながら解説していきます。

単利とは？

さて「単利」と「複利」という言葉を使いましたが、そもそも単利とは何を指すのでしょうか？単利とは、利息を計算する時に用いる計算方法の一つで、最初の元金（元本）にのみ利息がつくことをいいます。

仮に1万円を年利5％で預けると、一年後の元本と利息を合わせた金額は1万500円になります。単利だと2年目の利息も5％で500円ですので、元本と利息を合わせて残高は1万1000円となります。

複利とは？

続いて複利です。複利とは利息が元のお金（元本）に組み入れられ、それが次の利息が計算されるにあたって使われる元本となる計算式です。雪だるま式とも言えますが、簡単に言うと「利子が利子を呼ぶ」というようなイメージです。

複利の計算式の基本を知ろう

複利の計算式は数学記号で表示されることが多く、少々難しいです。そこで皆さんのお手元にある電卓で簡単に計算する方法をご紹介します。普通の電卓の他に、スマートフォンの電卓アプリでも可能なものが多いと思います。ただし電卓のメーカーにより入力方法が異なることもありますので、ご自身の電卓で二乗・三乗など計算を行うにはどのようにしたら良いかを確認してください。

例）10万円を年利5％で3年間、複利運用した際の満期時の元本と利息の合計を計算

ここでは大手メーカーの電卓を使っての計算方法を一例として使ってみます。

元金を1とします。利息が5%で0.05となり、1年目の元利合計は1＋0.05＝1.05です。
続いて電卓で下記の作業を行います。

1.    電卓に1.05と打ち込む
2.    次に×、×と2回入力
3.    ＝を一回入力すると・・・・・・・・・1.1025　　→2年目の元本の倍数
4.    ＝をさらにもう一回入力すると・・・・1.157625　→3年目の元本の倍数
5.　元金×倍数＝元利合計金額

上記の例題の場合は3年目の元利合計金額を求めるので、下記の式に当てはめます。

10万円×1.157625＝11万5672円というように計算できます。

パソコンの表計算ソフトなどが無くても、少し面倒ですが電卓でも計算できるということが分かるとイメージがしやすくなるのではないでしょうか。

＊計算機（電卓）のキー入力は、同メーカーであっても機種やシリーズ等で異なることがあります。ご確認ください。

単利と複利の効果の差／100万円を1年間運用した場合

単利と複利の違いが何となくイメージできたでしょうか？
この章では、100万円を単利と複利で運用したら元利合計の金額がどうなるかを試算していきます。

前提条件
資金：100万円　金利：年利5％　運用先：銀行に預ける

単利の場合
得られる利息→100万円×5％＝5万円
元本合計金額→100万円+5万円＝105万円

複利の場合
得られる利息→100万円×5％＝5万円
元本合計金額→100万円+5万円＝105万円

運用初年度に関しては運用に回す資金が100万円で同額ということもあり、違いはありませんでした。複利の「雪だるま式」・「利子が利子を呼ぶ」というのは運用期間が長期間になればなるほど効果を発揮します。次章ではさらに運用期間を延長した結果を試算して見ていきます。

単利と複利の効果の差／100万円を10年間運用した場合

この章では100万円を10年間運用し、単利と複利の違いがどれぐらい出るかを見ていきましょう。運用方式によってどれぐらいの差が出るかを見やすくするため、前提条件は先の例をそのまま流用してみます。

前提条件
資金：100万円　金利：年利5％　運用期間：10年間　運用先：銀行に預ける

単利の場合

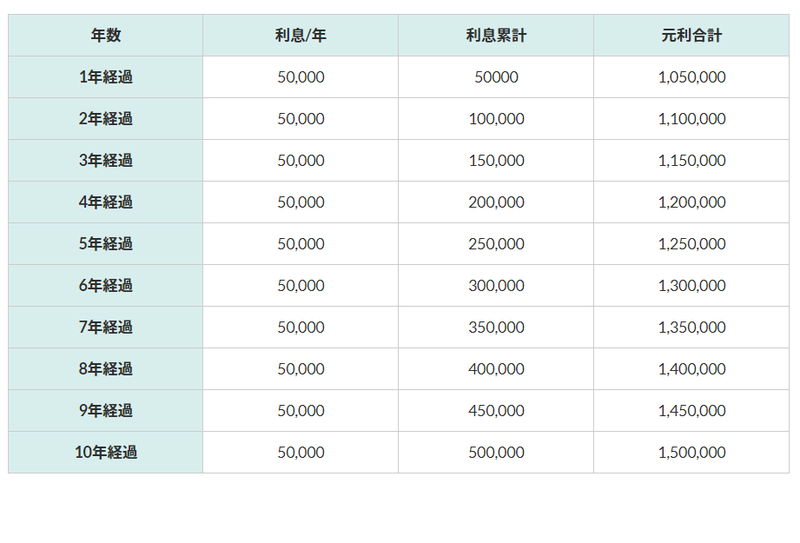
10年間の利息合計→　50万円　元利合計　150万円

どうでしょうか?
元本はそのまま、利息が毎年同じ金額で上乗せされています。

それでも「銀行の預金金利が0.001％」等の数字を見慣れてしまうと5％でも十分に見えてしまいますね。

次に複利の場合はどうなるでしょうか？

複利の場合

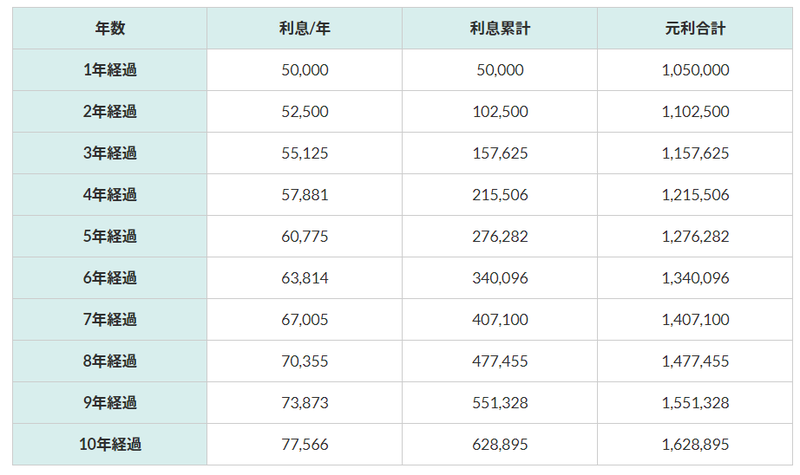
10年間の利息合計→　62万8895円　元利合計　162万8895円

いかがでしょうか？単利と複利で毎年の利息の増え方が異なり、元利合計の金額にも違いが出てきました。10年間で12万8895円の差なので、運用期間が長くなればさらに違いが出てきます。

複利の効果を最大にするのは「長期運用」

10年間で上記の差が出ていましたが、運用期間をさらに延ばして30年までをグラフにしてみましょう。

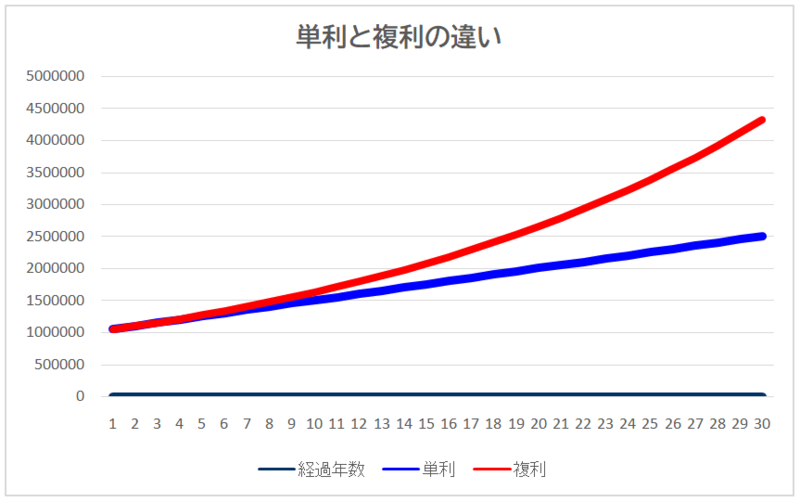
10年を経過したぐらいから差が拡大していき、15年を経過するとハッキリとした違いが見えてきます。イメージとして単利は足し算、複利は掛け算と言えるでしょう。

ちなみに100万円を年利5％で30年間運用した場合、単利であれば元利合計で250万円になります。複利で運用した場合の元利合計の金額は432万円まで増えます。スタート時の差は小さくても長期で運用すると大きな金額の違いになります。